Lessons of the ELB Most Complete From Sopintar
Lessons of the ELB Most Complete From Sopintar - Hello friend sopintar.blogspot.com SCIENCE & NEWS, In the article that you read this time with the title Lessons of the ELB Most Complete From Sopintar , we have prepared this article well for you to read and retrieve information in it. hopefully fill in the post
Artikel Academic Articles,
Artikel Economists,
Artikel Inflation,
Artikel Monetary Policy,
Artikel Nobel, what we write can you understand. OK, happy reading.
link : Lessons of the ELB Most Complete From Sopintar
I gave a short presentation on monetary policy at the Nobel Symposium run by the Swedish House of Finance. It was an amazing conference, and I'll post a blog review as soon as they get the slides up of the other talks. Offered 15 minutes to summarize what I know about the zero bound, as well as to comment on presentations by Mike Woodford and Stephanie Schmitt-Groh�, here is what I had to say. There is a pdf version here and slides here. Novelty disclaimer: Obviously, this involves a lot of recycling and digesting older material. But simplifying and digesting is a lot of what we do.
Update: video of the presentation here. Or hopefully the following embed works:
We just observed a dramatic monetary experiment. In the US, the short-term interest rate rate was stuck at zero for 8 years. Reserves rose from 10 billion to 3,000 billion. Yet inflation behaved in this recession and expansion almost exactly as it did in the previous one. The 10 year bond rate continued its gentle downward trend unperturbed by QE or much of anything else.
Europe's bound is ongoing with the same result.
Japan had essentially zero interest rates for 23 years. And..
Inflation stayed quiet and slightly negative the whole time. 23 years of the Friedman rule?
Our governments set off what should have been two monetary atomic bombs. Almost nothing happened. This experiment has deep lessons for monetary economics.
Stability Lessons
We learned that inflation can be stable and quiet--the opposite of volatile--in a long-lasting period of immobile interest rates, and with immense reserves that pay market interest.
The simplest theoretical interpretation is that inflation is stable under passive policy or even an interest rate peg. Alternative stories--it's really unstable but we had 23 years of bad luck--are really strained.
Stability is the central concept in my remarks today, and I emphasize it with the cute picture. If inflation is unstable, a central bank is like a seal balancing a ball on its nose. If inflation is stable, the bank is like Professor Calculus swinging his pendulum. Watching inflation and interest rates in normal times you cannot tell the seal from the Professor. Asking the professor might not help. Tintin fans will remember that the Professor, perhaps like the Fed, thought he was following the pendulum, not the other way around.
But if you hold still the seal's nose, or the professor's hand, you find out which is the case.
We just ran that experiment. The result: Inflation is stable. Many hallowed doctrines fall by the wayside.
Quantity lessons
We learn that arbitrary quantities of interest-paying reserves do not threaten inflation or deflation. We can live the Friedman-optimal quantity of money. There is no need to control the quantity of reserves. There is no reason for government debt to be artificially illiquid by maturity or denomination. Governments could offer reserve-like debt to all of us, essentially money market accounts. Too bad for contrary hallowed doctrines.
Interest rate lessons
The lessons for interest rate policy are even deeper.
\begin{align} x_t &= E_t x_{t+1} - \sigma(i_t - E_t\pi_{t+1} + v^r_t) \label{IS}\\ \pi_t &= E_t\pi_{t+1} + \kappa x_t \label{NK}\\ i_t &= \max\left[ i^\ast + \phi(\pi_t-\pi^\ast),0\right] \label{TR} \end{align} \begin{equation} (E_{t+1}-E_t) \pi_{t+1} = (E_{t+1}-E_t) \sum_{j=0}^\infty m_{t,t+j} s_{t+j}/b_t .\label{FTPL} \end{equation}
A common structure unites all the views I will discuss: An IS relation linking the output gap to real interest rates; a Phillips curve; a policy rule by which interest rates may react to inflation and output; and the government debt valuation equation, which states that an unexpected inflation or deflation, which changes the value of government bonds, must correspond to a change in the present value of surpluses
The equations are not at issue. All models contain these equations, including the last one. The issues are, How we solve, use, and interpret these equations? What is nature of expectations--adaptive, rational, or in between? How do we handle multiple equilibria? And what is the nature of fiscal/monetary coordination? Preview: that last one is the key to solving all the puzzles.
Adaptive Expectations / Old-Keynesian
The adaptive expectations view, from Friedman 1968 to much of the policy world today, makes a clear prediction: Inflation is unstable, so a deflation spiral breaks out at the lower bound. I simulate such a model in the graph. There is a negative natural rate shock; once the interest rate hits the bound, deflation spirals away.
The deflation spiral did not happen. This theory is wrong.
Rational Expectations / New-Keynesian I
The New Keynesian tradition uses rational expectations. Now the model is stable. That is a a big feather in the new-Keynesian cap.
But the new-Keynesian model only ties down expected inflation. Unexpected inflation can be anything. There are multiple stable equilibria, as indicated by the graph from Stephanie's famous JPE paper. This view predicts that the bound--or any passive policy--should feature sunspot volatility.
For example, Clarida Gal� and Gertler famously claimed that passive policy in the 70s led to inflation volatility, and active policy in the 1980s quieted inflation. A generation of researchers worried that Japan's zero bound, and then our own, must result in a resurgence of volatility.
It did not happen. Inflation is also quiet, and thus apparently determinate, at the bound. This theory is wrong--or at least incomplete.
New-Keynesian II Selection by future active policy
Another branch of new-Keynesian thinking selects among the multiple equilibria during the bound by expectations of future active policy.
To illustrate, this graph presents inflation in the simple new Keynesian model. There is a natural rate shock from time 0 to 5, provoking a zero bound during that period. There are multiple stable inflation equilibria.
The lower red equilibrium is a common choice, featuring a deep deflation and recession. To choose it, authors assume that after the bound ends, the central bank returns to active policy, threatening to explode the economy for any but its desired inflation target, zero here. Working back, we choose that one equilibrium during the bound.
Forward guidance
In this view small changes in expectations about future inflation work backwards to large changes at earlier times. Therefore, if the central bank promised inflation somewhat above target at the end of the bound, that promise would work its way back to large stimulus during the bound. Forward guidance offers strong stimulus.
One of Mike's main points today is that a price level target can help to enforce such a commitment. Stephanie's policy of raising rates to raise inflation at the end of the bound can similarly work its way back in time and stimulate during the the bound, perhaps avoiding the bound all together.
Forward guidance puzzles
This selection by future active policy, however, has huge problems. First, promises further in the future have larger effects today! I asked my wife if she would cook dinner if I promised to clean up 5 years from now. It didn't work.
Second, as we make prices less sticky, dynamics happen faster. So, though price stickiness is the only friction, making prices less sticky makes deflation and depression worse. The frictionless limit is negative infinity, though the frictionless limit point is small inflation and no recession. These problems are intrinsic to stability, and thus very robust: stable forward is unstable backward.
New Keynesian Solutions
The new-Keynesian literature is ripping itself apart to fix these paradoxes. Mike, Xavier Gabaix, and others abandon rational expectations. Alas even that step does not fix the problem.
Mike offers a k-step induction. It is complex. I spent over a month trying to reproduce a basic example of his method, and I failed. You have to be a lot smarter or more patient than me to use it. Moreover, it only reduces the magnitude of the backward explosion, not its fundamental nature.
If we go back to adaptive expectations, as Xavier and others do--after a similar hundred pages of difficult equations--then we're back to stable backward but explosive forward. Stable backward solves the forward guidance puzzle--but the lack of a spiral just told us inflation is stable forward. Also, you have to modify the model to the point that eigenvalues change from less to greater than one. It takes a discrete amount of irrationality to do that.
Fiscal theory of monetary policy
So let me unveil the answer. I call it the Fiscal Theory of Monetary Policy. The model is unchanged, but we solve it differently. We remove the assumption that surpluses ``passively'' accommodate any price level. Now, we pick equilibria by unexpected inflation, at the left side of the graph.
For example, an unexpected deflation can only happen if the government will raise taxes or cut spending to pay a windfall to bondholders. (Or, if discount rates raise the present value of surpluses, which is important empirically.) For example, if there is no fiscal news, we pick the equilibrium with the big red square at zero.
This is not some wild new theory. It is just a wealth effect of government bonds. We're replaying Pigou vs. Keynes, with much better equations.
The result is a model that is simple, stable, and solves all the puzzles.
Instantly, we know why the downward deflation jump did not happen. The great recession was not accompanied by a deflationary fiscal tightening!
Tying down the left end of the graph, promises further in the future have less effect today and there is a smooth frictionless limit. Tying down the left end of the graph stops backward explosions. You don't have to pick a particular value. The limits are cured if you just bound the size of fiscal surprises, and thus keep the jump on the left hand side from growing.
We can maintain rational expectations. This is not a religious commandment. Some irrational expectations are a fine ingredient for matching data and real-world policy; introducing some lags in the Phillips curve for example. But Mike's and others' effort to repair zero bound puzzles by irrational expectations is not such an epicycle. It asserts that the basic properties of monetary policy depend on people never catching on. It implies that all of economics and all of finance must abandon rational expectations even as rough approximations. Just to solve some murky paradoxes of new Keynesian models at the lower bound? For example, Andrei Shleifer, earlier today, argued for irrational expectations. But even he build on the efficient market rational expectation model, suggesting deviations from it. He did not require irrational expectations to begin to talk about asset pricing, or require that all of economics must adopt his form of irrational expectations.
I did not think the day would come that I would be defending the basic new-Keynesian program -- construct a model of monetary policy that plays by Lucas rules, or at least is a generalization of a model that does so -- and that Mike Woodford would be trying to tear it down. Yet here we are. Promote the fiscal equation from the footnotes and you can save the rest.
Neo-Fisherism
Neo-Fisherism is an unavoidable consequence of stability. If inflation is stable at a peg, then raising the interest rate and keeping it there must lead to higher inflation.
Conventional wisdom goes the other way. But it is still possible that higher interest rates temporarily lower inflation, accounting for that belief.
The standard new-Keyensian model, as illustrated in Harald and Marty's slides seems to achieve a temporary negative sign. However it only does so by marrying a fiscal contraction ("passively,'' but still there) to the monetary policy shock. It also requires an AR(1) policy disturbance -- beyond the AR(1) there is no connection between the permanence of the shock and the rise or decline of inflation.
Can we produce a negative sign from a pure monetary policy shock -- a rise in interest rates that does not coincide with fiscal tightening?
FTMP, long-term debt and a negative short run response
The fiscal theory of monetary policy can deliver that temporary negative effect with long term debt. The graph presents the price level, in a completely frictionless economy consisting only of a Fisher equation and the valuation equation. When nominal interest rates rise, the market value of debt on the left declines. (First line below graph.) If surpluses on the right do not change, the price level on the left must also decline. Then, the Fisherian positive effect kicks in.
FTMP, long-term debt, sticky prices and a realistic response
If you add sticky prices, then a rise in interest rates results in a smoothed out disinflation. This is a perfectly reasonable--but long-run Fisherian--response function.
Neofisherism?
In sum, the long-run Fisherian result is an inescapable consequence of stability.
The fiscal theory can give a temporary negative sign, but only if the interest rate rise is unexpected, credibly persistent, and there is long-term debt. Those considerations amplify Stephanie's call for gradual and pre-announced interest rate rises to raise inflation.
The contrast between the US, that followed Stephanie's advice and is now seeing a rise in inflation, with Japan and Europe, is suggestive.
The negative sign in the standard new-Keynesian model comes by assuming a fiscal contraction coincident with the monetary policy shock.
Beware! These arguments do not mean that high inflation countries like Brazil, Turkey, and Venezuela can simply lower rates to lower inflation. Everything here flows from fiscal foundations, and absent fiscal foundations and commitment to permanently lower rates, inflation is inevitable.
Advertisements
I promised that the ELB was an experiment that would deliver deep implications for monetary policy. Think of the hallowed doctrines that have been overturned in the last 15 minutes.
What I've said today, and the graphs, are in these references. They go on to show you how the fiscal theory of monetary policy provides a simple unified framework for interest rate policy, quantitative easing, and forward guidance, that works even in frictionless models, though price stickiness is useful to produce realistically slow dynamics.
link : Lessons of the ELB Most Complete From Sopintar
I gave a short presentation on monetary policy at the Nobel Symposium run by the Swedish House of Finance. It was an amazing conference, and I'll post a blog review as soon as they get the slides up of the other talks. Offered 15 minutes to summarize what I know about the zero bound, as well as to comment on presentations by Mike Woodford and Stephanie Schmitt-Groh�, here is what I had to say. There is a pdf version here and slides here. Novelty disclaimer: Obviously, this involves a lot of recycling and digesting older material. But simplifying and digesting is a lot of what we do.
Update: video of the presentation here. Or hopefully the following embed works:
Lessons of the long quiet ELB
(effective lower bound)
(effective lower bound)
We just observed a dramatic monetary experiment. In the US, the short-term interest rate rate was stuck at zero for 8 years. Reserves rose from 10 billion to 3,000 billion. Yet inflation behaved in this recession and expansion almost exactly as it did in the previous one. The 10 year bond rate continued its gentle downward trend unperturbed by QE or much of anything else.
Europe's bound is ongoing with the same result.
 |
| Source: Stephanie Schmitt-Groh� |
 |
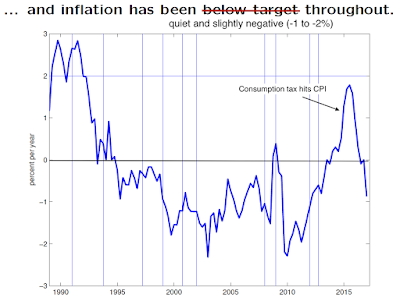| Source: Stephanie Schmitt-Groh� |
Inflation stayed quiet and slightly negative the whole time. 23 years of the Friedman rule?
Our governments set off what should have been two monetary atomic bombs. Almost nothing happened. This experiment has deep lessons for monetary economics.
Stability Lessons
We learned that inflation can be stable and quiet--the opposite of volatile--in a long-lasting period of immobile interest rates, and with immense reserves that pay market interest.
The simplest theoretical interpretation is that inflation is stable under passive policy or even an interest rate peg. Alternative stories--it's really unstable but we had 23 years of bad luck--are really strained.
Stability is the central concept in my remarks today, and I emphasize it with the cute picture. If inflation is unstable, a central bank is like a seal balancing a ball on its nose. If inflation is stable, the bank is like Professor Calculus swinging his pendulum. Watching inflation and interest rates in normal times you cannot tell the seal from the Professor. Asking the professor might not help. Tintin fans will remember that the Professor, perhaps like the Fed, thought he was following the pendulum, not the other way around.
But if you hold still the seal's nose, or the professor's hand, you find out which is the case.
We just ran that experiment. The result: Inflation is stable. Many hallowed doctrines fall by the wayside.
Quantity lessons
 |
| The optimal quantity of money |
Interest rate lessons
The lessons for interest rate policy are even deeper.
\begin{align} x_t &= E_t x_{t+1} - \sigma(i_t - E_t\pi_{t+1} + v^r_t) \label{IS}\\ \pi_t &= E_t\pi_{t+1} + \kappa x_t \label{NK}\\ i_t &= \max\left[ i^\ast + \phi(\pi_t-\pi^\ast),0\right] \label{TR} \end{align} \begin{equation} (E_{t+1}-E_t) \pi_{t+1} = (E_{t+1}-E_t) \sum_{j=0}^\infty m_{t,t+j} s_{t+j}/b_t .\label{FTPL} \end{equation}
A common structure unites all the views I will discuss: An IS relation linking the output gap to real interest rates; a Phillips curve; a policy rule by which interest rates may react to inflation and output; and the government debt valuation equation, which states that an unexpected inflation or deflation, which changes the value of government bonds, must correspond to a change in the present value of surpluses
The equations are not at issue. All models contain these equations, including the last one. The issues are, How we solve, use, and interpret these equations? What is nature of expectations--adaptive, rational, or in between? How do we handle multiple equilibria? And what is the nature of fiscal/monetary coordination? Preview: that last one is the key to solving all the puzzles.
Adaptive Expectations / Old-Keynesian
The deflation spiral did not happen. This theory is wrong.
Rational Expectations / New-Keynesian I
But the new-Keynesian model only ties down expected inflation. Unexpected inflation can be anything. There are multiple stable equilibria, as indicated by the graph from Stephanie's famous JPE paper. This view predicts that the bound--or any passive policy--should feature sunspot volatility.
For example, Clarida Gal� and Gertler famously claimed that passive policy in the 70s led to inflation volatility, and active policy in the 1980s quieted inflation. A generation of researchers worried that Japan's zero bound, and then our own, must result in a resurgence of volatility.
It did not happen. Inflation is also quiet, and thus apparently determinate, at the bound. This theory is wrong--or at least incomplete.
New-Keynesian II Selection by future active policy
Another branch of new-Keynesian thinking selects among the multiple equilibria during the bound by expectations of future active policy.
To illustrate, this graph presents inflation in the simple new Keynesian model. There is a natural rate shock from time 0 to 5, provoking a zero bound during that period. There are multiple stable inflation equilibria.
The lower red equilibrium is a common choice, featuring a deep deflation and recession. To choose it, authors assume that after the bound ends, the central bank returns to active policy, threatening to explode the economy for any but its desired inflation target, zero here. Working back, we choose that one equilibrium during the bound.
Forward guidance
In this view small changes in expectations about future inflation work backwards to large changes at earlier times. Therefore, if the central bank promised inflation somewhat above target at the end of the bound, that promise would work its way back to large stimulus during the bound. Forward guidance offers strong stimulus.
One of Mike's main points today is that a price level target can help to enforce such a commitment. Stephanie's policy of raising rates to raise inflation at the end of the bound can similarly work its way back in time and stimulate during the the bound, perhaps avoiding the bound all together.
Second, as we make prices less sticky, dynamics happen faster. So, though price stickiness is the only friction, making prices less sticky makes deflation and depression worse. The frictionless limit is negative infinity, though the frictionless limit point is small inflation and no recession. These problems are intrinsic to stability, and thus very robust: stable forward is unstable backward.
New Keynesian Solutions
The new-Keynesian literature is ripping itself apart to fix these paradoxes. Mike, Xavier Gabaix, and others abandon rational expectations. Alas even that step does not fix the problem.
Mike offers a k-step induction. It is complex. I spent over a month trying to reproduce a basic example of his method, and I failed. You have to be a lot smarter or more patient than me to use it. Moreover, it only reduces the magnitude of the backward explosion, not its fundamental nature.
If we go back to adaptive expectations, as Xavier and others do--after a similar hundred pages of difficult equations--then we're back to stable backward but explosive forward. Stable backward solves the forward guidance puzzle--but the lack of a spiral just told us inflation is stable forward. Also, you have to modify the model to the point that eigenvalues change from less to greater than one. It takes a discrete amount of irrationality to do that.
Fiscal theory of monetary policy
For example, an unexpected deflation can only happen if the government will raise taxes or cut spending to pay a windfall to bondholders. (Or, if discount rates raise the present value of surpluses, which is important empirically.) For example, if there is no fiscal news, we pick the equilibrium with the big red square at zero.
This is not some wild new theory. It is just a wealth effect of government bonds. We're replaying Pigou vs. Keynes, with much better equations.
The result is a model that is simple, stable, and solves all the puzzles.
Instantly, we know why the downward deflation jump did not happen. The great recession was not accompanied by a deflationary fiscal tightening!
Tying down the left end of the graph, promises further in the future have less effect today and there is a smooth frictionless limit. Tying down the left end of the graph stops backward explosions. You don't have to pick a particular value. The limits are cured if you just bound the size of fiscal surprises, and thus keep the jump on the left hand side from growing.
We can maintain rational expectations. This is not a religious commandment. Some irrational expectations are a fine ingredient for matching data and real-world policy; introducing some lags in the Phillips curve for example. But Mike's and others' effort to repair zero bound puzzles by irrational expectations is not such an epicycle. It asserts that the basic properties of monetary policy depend on people never catching on. It implies that all of economics and all of finance must abandon rational expectations even as rough approximations. Just to solve some murky paradoxes of new Keynesian models at the lower bound? For example, Andrei Shleifer, earlier today, argued for irrational expectations. But even he build on the efficient market rational expectation model, suggesting deviations from it. He did not require irrational expectations to begin to talk about asset pricing, or require that all of economics must adopt his form of irrational expectations.
I did not think the day would come that I would be defending the basic new-Keynesian program -- construct a model of monetary policy that plays by Lucas rules, or at least is a generalization of a model that does so -- and that Mike Woodford would be trying to tear it down. Yet here we are. Promote the fiscal equation from the footnotes and you can save the rest.
Neo-Fisherism
Neo-Fisherism is an unavoidable consequence of stability. If inflation is stable at a peg, then raising the interest rate and keeping it there must lead to higher inflation.
The standard new-Keyensian model, as illustrated in Harald and Marty's slides seems to achieve a temporary negative sign. However it only does so by marrying a fiscal contraction ("passively,'' but still there) to the monetary policy shock. It also requires an AR(1) policy disturbance -- beyond the AR(1) there is no connection between the permanence of the shock and the rise or decline of inflation.
Can we produce a negative sign from a pure monetary policy shock -- a rise in interest rates that does not coincide with fiscal tightening?
FTMP, long-term debt and a negative short run response
The fiscal theory of monetary policy can deliver that temporary negative effect with long term debt. The graph presents the price level, in a completely frictionless economy consisting only of a Fisher equation and the valuation equation. When nominal interest rates rise, the market value of debt on the left declines. (First line below graph.) If surpluses on the right do not change, the price level on the left must also decline. Then, the Fisherian positive effect kicks in.
FTMP, long-term debt, sticky prices and a realistic response
If you add sticky prices, then a rise in interest rates results in a smoothed out disinflation. This is a perfectly reasonable--but long-run Fisherian--response function.
Neofisherism?
In sum, the long-run Fisherian result is an inescapable consequence of stability.
The fiscal theory can give a temporary negative sign, but only if the interest rate rise is unexpected, credibly persistent, and there is long-term debt. Those considerations amplify Stephanie's call for gradual and pre-announced interest rate rises to raise inflation.
The contrast between the US, that followed Stephanie's advice and is now seeing a rise in inflation, with Japan and Europe, is suggestive.
The negative sign in the standard new-Keynesian model comes by assuming a fiscal contraction coincident with the monetary policy shock.
Beware! These arguments do not mean that high inflation countries like Brazil, Turkey, and Venezuela can simply lower rates to lower inflation. Everything here flows from fiscal foundations, and absent fiscal foundations and commitment to permanently lower rates, inflation is inevitable.
Advertisements
I promised that the ELB was an experiment that would deliver deep implications for monetary policy. Think of the hallowed doctrines that have been overturned in the last 15 minutes.
- "The New-Keynesian Liquidity Trap'' December 2018 Journal of Monetary Economics 92, 47-63.
- "Michelson-Morley, Fisher, and Occam: The Radical Implications of Stable Inflation at the Zero Bound" Macroeconomics Annual 2018.
- "Stepping on a Rake: the Fiscal Theory of Monetary Policy'' January 2018. European Economic Review 101, 354-375.
What I've said today, and the graphs, are in these references. They go on to show you how the fiscal theory of monetary policy provides a simple unified framework for interest rate policy, quantitative easing, and forward guidance, that works even in frictionless models, though price stickiness is useful to produce realistically slow dynamics.
This is the article Lessons of the ELB Most Complete From Sopintar
So many articles Lessons of the ELB Most Complete From Sopintar this time, hopefully it can benefit you all. OK, see you in another article.